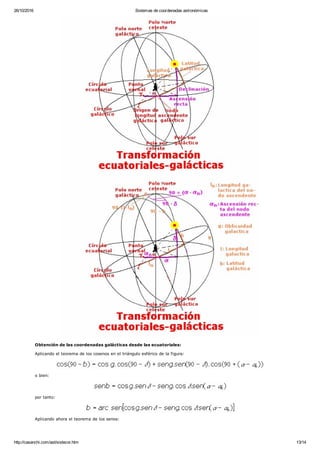
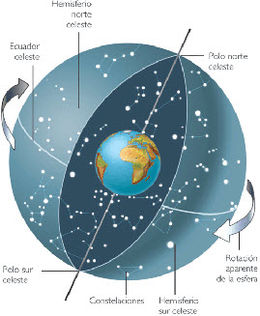
Se trata de convertir coordenadas celestes de un tipo en otro.

Las fórmulas

Las fórmulas para convertir las coordenadas ecuatoriales en coordenadas galácticas son:

  • cos ⁡ b cos ⁡ ( l − l n ) = cos ⁡ δ cos ⁡ ( α − α n ) {\displaystyle \cos b\cos(l-l_{n})=\cos \delta \cos(\alpha -\alpha _{n})\,} (1)
  • sin ⁡ b = sin ⁡ δ cos ⁡ g − cos ⁡ δ sin ⁡ g sin ⁡ ( α − α n ) {\displaystyle \sin b=\sin \delta \cos g-\cos \delta \sin g\sin(\alpha -\alpha _{n})\,} (2)
  • cos ⁡ b sin ⁡ ( l − l n ) = sin ⁡ δ sin ⁡ g cos ⁡ δ cos ⁡ g sin ⁡ ( α − α n ) {\displaystyle \cos b\sin(l-l_{n})=\sin \delta \sin g \cos \delta \cos g\sin(\alpha -\alpha _{n})\,} (3)


donde α {\displaystyle \alpha } es la ascensión recta, δ {\displaystyle \delta } es la declinación, l {\displaystyle l} es la longitud galáctica y b {\displaystyle b} es la latitud galáctica. Las constantes introducidas valen α n = 282 , 25 ∘ {\displaystyle \alpha _{n}=282{,}25^{\circ }} , l n = 33,012 ∘ {\displaystyle l_{n}=33{,}012^{\circ }} y g = 62 , 6 ∘ {\displaystyle g=62{,}6^{\circ }}

El cálculo y resolución de ambigüedades

De la ecuación (2) se obtiene mediante la función arcsin {\displaystyle \arcsin \,} la latitud galáctica b {\displaystyle b} sin ambigüedad.

  • Hay que tener presente que g = 62 , 6 ∘ {\displaystyle g=62{,}6^{\circ }} es complementario del valor utilizado en el applet 27,4º por lo que sin ⁡ g = cos ⁡ 27 , 4 ∘ {\displaystyle \sin g=\cos 27{,}4^{\circ }} y cos ⁡ g = sin ⁡ 27 , 4 ∘ {\displaystyle \cos g=\sin 27{,}4^{\circ }} . Por otra parte α n {\displaystyle \alpha _{n}} y 192,25 que es el valor usado en el applet difieren en 90°, y que cos ⁡ ( x 90 ∘ ) = − sin ⁡ ( x ) {\displaystyle \cos(x 90^{\circ })=-\sin(x)\,} .
  • Dividiendo (3)/(1) y sustituyendo (2) puede obtenerse:
tan ⁡ ( l − l n ) = sin ⁡ δ − cos ⁡ g ⋅ sin ⁡ b sin ⁡ g ⋅ cos ⁡ δ ⋅ cos ⁡ ( α − α n ) {\displaystyle \tan(l-l_{n})={\frac {\sin \delta -\cos g\cdot \sin b}{\sin g\cdot \cos \delta \cdot \cos(\alpha -\alpha _{n})}}\,}
  • Recordando que g {\displaystyle g\,} y 27,4 son complementarios y que sin ⁡ ( x 90 ∘ ) = cos ⁡ ( x ) {\displaystyle \sin(x 90^{\circ })=\cos(x)\,} obtenemos la fórmula programada para obtener l − l n {\displaystyle l-l_{n}\,}

Un applet en Java-Script

Un script de Java[1] que hace esto es:

Véase también

  1. Coordenadas celestes
  2. Conversión de coordenadas eclípticas a coordenadas ecuatoriales
  3. Conversión de coordenadas ecuatoriales a coordenadas eclípticas
  4. Conversión de coordenadas ecuatoriales a coordenadas horarias
  5. Conversión de coordenadas ecuatoriales a coordenadas horizontales
  6. Conversión de coordenadas horizontales a coordenadas ecuatoriales
  7. Conversión de coordenadas galácticas a coordenadas ecuatoriales
  8. Conversión de coordenadas horarias a coordenadas horizontales
  9. Conversión de coordenadas horizontales a coordenadas horarias

Física y Astronomía Esfera celeste y Sistemas de coordenadas

Sistemas de coordenadas astronómicas PDF

Coordenadas astronómicas Page 2 Austrinus

Coordenadas celestes EcuRed

Conversion De Coordenadas Polares A Rectangulares Eje vrogue.co